Tatár László

Bayes' Theorem As A Method Of Interpreting Criminal Evidence

 

Collecting evidence is an evergreen problem of the sciences of criminal procedure law (1). The problem is originated on the one hand from the fact, that in the criminal proceedings there is a lack of evidences in a typical case. It is to understand, when the practicant of law is seeking to use the few available evidences at the highest efficiency level. The other side of the problem is, that by interpreting evidence the practicant of law draws conclusions as part of the interpretation of evidences, and he defines the facts of the case based on this conclusions. When is to consider, that we have enough evidences, and what method shall we use to interpret this evidences? The most efficient method we use, it is more probable that we will define the correct facts of the case. But is there any method, which leads us inerrable to the correct facts of the case, or with other words which helps us to draw the right conclusion from the given evidence? There is a discussion about a method in the foreign literature (2), which insert the evidences in a mathematical equation and it defines the value of the evidences upon that.

The beginnings of the method go back to the XVIII century. The essay of Thomas Bayes (1702-1761) - british presbyterian minister, mathematician - about the theory of probability was found among his papers after his death by one of his friends and this friend sent it to the Royal Society of London which published it. (3). Bayes intended to create a method which enables to determine the probability of the occurrence of an event, about which we know nothing, but how many times it had happen and how many times it had fail under the given circumstances. Bayes created a formula, which shows the events in mathematical correlation and in the end it gives a numerical value of the probability of occurring an event. The method known as Bayes' Theorem is used in many fields of science.

Bayes' Theorem can play an important role in criminal proceedings mainly by evaluating of circumstantial evidences. Using Bayes' formula after examining some probability information we get an answer to the question, how the primary probability of an event (guilt of the suspect) changes if there is a given circumstance (circumstantial evidence). So it shows how the given circumstantial evidence increases or decreases the probability of the fact, that the suspect committed the crime.

The formula of Bayes:

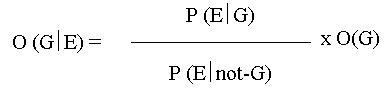
O = odds

P = probability

G = guilt

E = evidence

not-G = not guilty

O (G ï E) = chance of the guilt of the suspect given the evidence we are examining (a-posteriori chance)

P (E ï G) = probability of occurring the evidence when suspect is guilty

P (E ï not-G) = probability of occurring the evidence when suspect is not guilty

O(G) = chance of the guilt of the suspect before examining the given evidence (a-priori chance)

Probability is the rational degree of the confidence of the truth of the assertion based on the given information (evidence). An assertion can be true or false, but we are not sure if it is true or false. The value of every probability depends on the information used to define it (4). By using the formula the value of probability will stay every time between 0 and 1. If the value of probability is 0, it means, that the assertion is - with full certainty - absurd, false. If the value of probability is 1, it means, that the assertion is - with full certainty - true. The value of probability is in most cases between these two values. (Expressed in percentage, by a probability value of 0 is the probability of the truth of the assertion 0 %, and by a probability value of 1 is the probability of the truth of the assertion 100 %.) When the probability value is 0.5, the probability of the truth of the assertion is the same as the probability of the falsehood of that assertion. (In percentage the probability can be expressed as 50 %.)

Chance gives us the answer to our proper question. The question in the criminal procedure, to that we search for an answer using Bayes' Theorem is: How much is the chance of the suspect's guilt? But this formula doesn't decide about the suspect's guilt, it only shows, that the analysed evidence increases or decreases the chance of the suspect's guilt. To this operation we need the value of the a-priori chance. We have to define this. This means, we have to convert our non-numerical facts or the conclusions from those facts to numbers. The definition of the value of the a-priori chance influences basically our final value (the a-posteriori chance). The definition of the a-priori chance is the critical part of using Bayes' Theorem. If we make a mistake at this point, then we wouldn't gain the correct value of the a-posteriori chance also.

Practically the formula works us out, how the chance of the suspect's guilt without examining the given evidence changes after having been examined the given evidence. The probability of the truth of the analysed assertion can be described as the relation of the value of the a-posteriori chance [ O (G ï E) ] and 1. If the value of the a-posteriori chance is 1, it means, that the suspect's guilt has the same probability as the suspect's innocence. (1:1, the chance of the suspect's guilt is 50 %). If the value of the a-posteriori chance is smaller than 1, it means, that the suspect’s innocence is more probable, than his guilt. (pl. 0.75:1 (5), or 3:4 (6), the chance of the suspect's guilt is 42.9 %). If the value of the a-posteriori chance is higher than 1, it means, that the suspects guilt is more probable, than his innocence. (e.g. 2:1, the chance of the suspect's guilt is 66.7 %).

It is very important, that we don't mix up probability and chance! The value of probability lies every time between 0 and 1, but the value of chance can be 0 and any other number greater than 0 (the higher is the value of chance, the probable is the truth of our assertion analysed by the Bayes' formula). Mathematically there is the following connection between chance and probability:

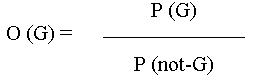
The perpetrator cut himself by a homicide in Auckland, so there remain blood residues at the crime scene. In the criminal trial (7) conducted in New-Zealand the forensic expert, who performed the DNA-analysis of the blood residue, declared, that the probability of the blood residue found at the crime scene being from the suspect is 12450 times higher, than being from another person. Saying with other words: there is 1 person among 12450 persons, who has the given DNA-profile. The expert had given with this the likelihood ratio of the analysed evidence (expert's opinion):

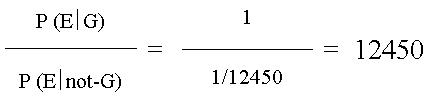
This likelihood ratio shows us, what effect the given evidence has on the probability of the suspect's guilt. This value has to be multiplied with the a-priori chance [ O (G) ] to get the a-posteriori chance [ O (G ï E) ] . The more differs the likelihood ratio from 1 - in any direction -, the bigger will be it's effect on the probability of the suspect's guilt. In the case, when the value of the likelihood ration doesn't differ from 1, or doesn't differ significantly from 1, the evidence has no effect or no significant effect on the outcome of the evidentiary process.

In common law legal systems evidence with a likelihood ratio of 1 or close to 1 is considered to not relevant evidence, and so it is not admissible at trial (8). Purpose of excluding this evidence is to prevent the jurors from being misled by deciding the question of the suspect's guilt. In cases like that the judge doesn't permit to show the evidence to the jurors, or if it was already shown to them, the judge instructs the jurors not to consider the evidence by the decision making. It is not uncommon, that courts consider evidences with likelihood ratio under 100 as almost unuseful (9).

Back to our example, to make Bayes' formula complete, we need the value of the a-priori chance of the suspect's guilt. [ O (G) ] . We have to define the numerical value of this chance. Considering that the population of Auckland is approximately 1,000,000 persons, we should take the a-priori chance of the suspect's guilt for 1:999,999 (10). This a-priori chance means, that from 1,000,000 persons there is 1 guilty person and 999,999 innocent persons. (11). (It is to see, that defining the a-priori chance is not fully objective, because the perpetrator was not necessarily living in Auckland. As we haven't examined any other evidences yet, we have no other information from the case, we should start with this value!) In the Bayes' formula:

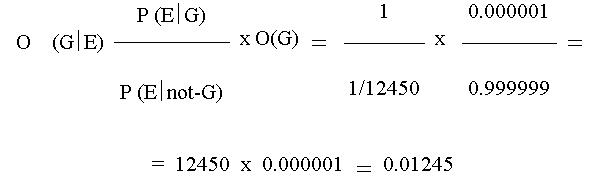
The outcome of analysing the DNA profile has increased the a-priori chance - defined by us - of the suspect's guilt significantly (from 0.000099 % to 1.230 % (12)), but the chance that the suspect had committed the crime is even at this stage only 1.230 %.

In that case the court has had also another evidence, which indicated, that the perpetrator was member of a small group of 5 persons. The suspect was also member of this group. Upon that evidence - supposing that it narrows the number of the suspects leaving no doubt - the a-priori chance that the suspect was the perpetrator is significantly higher, exactly 1:4 (13), or 20 %. Let's see the effect of the expert's opinion on this a-priori chance (14):

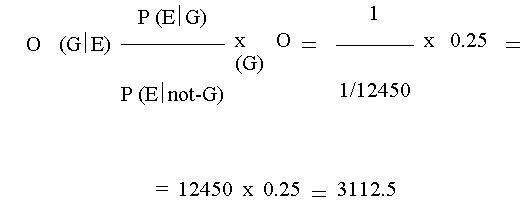
Thus the a-posteriori chance of the suspect's guilt is 3112.5:1, or expressed otherwise: 99.968 % (15). We did the same, as by the first calculation, where the outcome was 1.2 %, we calculated the effect of the expert's opinion to the suspect's guilt. Only the value of the a-priori chance was different. It is easy to understand, how important it is to define the value of the a-priori chance properly. In my opinion this is the critical point of using Bayes' Theorem in a criminal procedure. If we take a false value at this point, the outcome of using the Bayes' formula will be also false.

In another criminal case (16), the owner caught three burglars and it came to fighting. In the fight one of the burglars knocked the owner down. The burglar, who was hitting the owner, was light injured, so he left blood residues on the crime scene. While escaping one of the burglars was captured by the police. Blood-group of the blood residue found on the crime scene was B. The blood-group of the captured burglar was also B. How much is the chance upon the known evidences, that the owner was knocked down by the captured burglar? To the calculation we use the information, that 13 % of the population has blood-group B. Three persons could commit the crime: the 3 burglars. The a-priori chance that the owner was knocked down by the captured burglar is 1:2, which can be expressed as 0.5 (33.3 %). Probability of the blood mark to occur when the suspect is not guilty is 0.13.

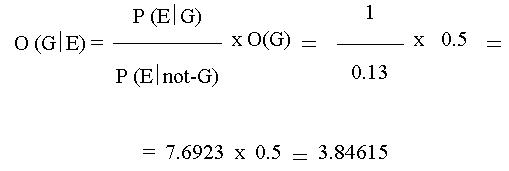
As result of the blood examination the chance, that the owner was knocked down by the captured burglar is 3.84615:1, which can be expressed as 79.36 % (17). The a-priori chance (33.3 %) was significantly increased as a result of the expert's opinion about the examination of the blood mark.

As the examples above concern the evaluation of the expert's opinion in a criminal case, major area of using Bayes' Theorem in a criminal procedure is the evaluation, interpretation of expert's opinions. The cases above show, that the correctness of the a-posteriori chance about the suspect's guilt, which we get as a result of applying Bayes' Theorem, depends on the information used by applying the Bayes-formula.

To the calculation we have to define two values. One of them is the likelihood ratio, the other is the a-priori chance of the suspect's guilt. To define the likelihood ratio is the task of the forensic expert, to define the a-priori chance and to calculate the a-posteriori chance applying the Bayes-formula and using the likelihood ratio defined by the forensic expert is the task of the court. The advantage of the Bayesian approach is, that it helps by systematisation of evidences (18).

Bayes' Theorem can be very helpful, as a method of interpreting, evaluating evidences, because it gives an objective tool, the Bayes-formula. But this method mustn't be over-estimated; it can't serve as a one and only method of interpreting every evidences or under any circumstances. It's major advantage is the objectivity, which helps the practicant of law – at the end the court deciding about the suspect's guilt - to come to the correct conclusions from the available evidences. The Bayes-formula shows the mathematical probability of the suspect's guilt given the examined evidence. In Hungary the court doesn't decide the question of the suspect's guilt on the basis of mathematical probability, but on the basis of explained confidence (19). It is necessary to the conviction of the suspect, that the judge is confident, that the suspect had committed the crime. Confidence is an intellectual-psychical phenomenon, and by every person there is another amount of evidences, information needed to reach the same confidence in the same question. This is why confidence has to be explained, it becomes so able to get controlled, if the court recognized the right aspects, and if the court considered the right aspects properly.

We would never get unshakeable certainty, confidence on the basis of mathematical probability. Theoretically there is a possibility for that [P (E ï G) = 1], but we would never get this value using the Bayes-formula by the interpretation of evidence. For example, when a security camera records the perpetrator committing the crime, and the perpetrator is clear to identify on basis of the recording without any doubt, we have to consider calculating mathematical probability, that the recording could also be a fake. Because of that the value of P (E ï G) will never be 1 in a criminal proceeding, in this case we can take it for instance for 0.98, so there is a mathematical probability of the suspect's innocence. Forensic experts can then examine, if the videotape is genuine or a fake, but this examinations have also a failure quotient. So when the forensic expert states, that the videotape is genuine, the mathematical probability of the guilt of the suspect recognized on the tape increases, but it will not reach 1 (it will be e. g. 0.s99), and it will never reach the value of 1. On the other hand, if the suspect can be recognized on the videotape as the perpetrator of the crime, this recording alone can be enough to make the judge confident about the suspect's guilt. So the judge can become confident, however the mathematical probability of the suspect's guilt is "only" 99 %.

But there is also an example of the contrary. In our second cited criminal case the mathematical probability that the captured burglar had knocked down the owner is 79 %. The probability of the suspect's guilt is higher, than the probability of his innocence. But if his two companions will be captured by the police, and one of them or both have the blood-group B, the mathematical probability, that the first suspect had knocked down the owner, will just decrease significantly.

As the examples show, a criminal case can't be solved only with mathematical methods. The unshakeable confidence of the judge can be reached at a mathematical probability with a value under 1 (moreover will the mathematical probability never reach the 100 %), and the unshakeable confidence of the judge doesn't have to be reached necessarily even at a relatively high level of mathematical probability. The reason for that is the method we use to get to the outcome. When calculating mathematical probability we insert the information we know into the formula, and after finishing the operation, we get the value of the mathematical probability. When looking for confidence the practicant of law reconstructs the happenings on the basis of the available evidences, he imagines what had happened. When about certain details of the facts (e. g. the identity of the perpetrator) there are more versions available (someone else could be also the perpetrator), and the available evidences doesn't exclude one of the versions, then the collecting of evidences has to be continued, till we got to a situation, where all the available evidences support only one version of facts and exclude all other versions of facts (it couldn't happened somehow else).

Mathematical methods can however very helpful by interpreting and evaluating evidences, they can help, but only when properly used (20), to get to the right conclusions on the basis of the evidences. The most significance can Bayes' Theorem have by interpreting the results of complex forensic expert examinations, however it can be used theoretically by interpreting any evidence.

---

Endnotes:

1 Flórián Tremmel: Magyar büntetőeljárás [Hungarian Criminal Procedure], Dialóg-Campus Kiadó, Budapest-Pécs, 2001, 207. p.

2 The court can prohibit the jurors from regarding the testimony of the expert witness about Bayes' Theorem at the time of the decision-making. The argument of exclusion was for example in the case Adams (Adams [1996] 2 Cr.App.R. 467.), that the interpretation of the evidence is the task of the jurors, and Bayes' Theorem is a scientific method, which is not appropriate for evaluating the evidences, so the jurors can't regard the testimony of the expert witness about Bayes' Theorem. (Bernard Robertson, Tony Vignaux: Bayes' Theorem in the Court of Appeal, in: The Criminal Lawyer, January, 1997, pp 4-5., source: http://www.mcs.vuw.ac.nz/~vignaux/docs/Adams_NLJ.html ). The exclusion of evidences like that developed in the common law legal system in order to prevent the jurors from being "mislead" by the expert witnesses. The Criminal Procedure Act of Hungary doesn't exclude the use of Bayes' Theorem by evaluating the evidences in criminal procedures.

3 An Essay towards solving a Problem in the Doctrine of Chances, in: Philosophical Transactions of the Royal Society of London, 1764

4 Bernard Robertson, G A Vignaux: Interpreting Evidence: Evaluating Forensic Science in the Courtroom,
John Wiley and Sons, 1995, source: http://www.mcs.vuw.ac.nz/~vignaux/evidence/interpreting.html 4. o.

5 Read as: zero point seventy-five to one

6 Read as: three to four

7 [ 1992 ] 1 NZLR 545 (CA)

8 Federal Rules of Evidence – USA

Rule 401. Definition of ''Relevant Evidence''

‘‘Relevant evidence’’ means evidence having any tendency to make the existence of any fact that is of consequence to the determination of the action more probable or less probable than it would be without the evidence.

Rule 402. Relevant Evidence Generally Admissible; Irrelevant Evidence Inadmissible

All relevant evidence is admissible, except as otherwise provided by the Constitution of the United States, by Act of Congress, by these rules, or by other rules prescribed by the Supreme Court pursuant to statutory authority. Evidence which is not relevant is not admissible.

9 Bernard Robertson, G A Vignaux: Interpreting Evidence: Evaluating Forensic Science in the Courtroom, John Wiley and Sons, 1995, source: http://www.mcs.vuw.ac.nz/~vignaux/evidence/interpreting.html, 11. p.

10 Bernard Robertson, G A Vignaux: Interpreting Evidence: Evaluating Forensic Science in the Courtroom, John Wiley and Sons, 1995, in: http://www.mcs.vuw.ac.nz/~vignaux/evidence/interpreting.html, 13. p.

Read as: one to nine hundred ninety-nine thousand nine hundred ninety-nine

11 Thus the a-priori chance of the suspect being the perpetrator is 1/1,000,000, and the a-priori chance of the suspect not beeing the perpetrator is 999,999/1,000,000.

12 0.01245/(0.01245+1)=0.1230

13 Read as: one to four

14 O (G)= P (G) / P (not-G) = 1 / 4 = 0.25

15 3112.5/(3112.5+1)=0.99968 Þ 99.968 %

16 Ralf Neuhaus: Kriminaltechnik für den Strafverteidiger – Eine Einführung in die Grundlagen 2. Teil Befundbewertung, in: Strafverteidiger Forum, 2001/4. source: http://www.ag-strafrecht.de/aufsatzneuhaus.htm

17 3.84615/(3.84615+1)=79.36 %

18 Encyclopedia of Forensic Sciences (ed.: Jay A. Siegel, Pekka J. Saukko, Geoffrey C. Knupfer), Academic Press 2000, New York, 718. p.

19 Flórián Tremmel: Magyar büntetőeljárás [Hungarian Criminal Procedure], Dialóg-Campus Kiadó, Budapest-Pécs, 2001, 213. p.

20 See e.g.: definition of the value of the a-priori chance